Menschenbegriff
Wie verhältsich die Menge der Personen zur Menge der Menschen und umgekehrt?
Die angesprochenen Fragen
und insbesondere die Frage, ob alle Menschen Personen sind oder nicht,
können, noch bevor es zu einer materialen Untersuchung kommt, rein formallogisch
bzw. mengentheoretisch untersuchtwerden. Eine formale bzw. mengentheoretisch
vollständige Untersuchung (was die mengentheoretischenAntwortmöglichkeiten
betrifft) der „Beziehung der Begriffe ‘Mensch’ und ‘Person’“ hat
Christian Erk unternommen. Die Hauptergebnisse dieser Untersuchung sollen
im Folgenden zusammenfassend wiedergeben werden. Mit Erk können also alle logischen bzw. mengentheoretisch möglichen Varianten der begrifflichen
Beziehung zwischen dem Begriff Mensch und dem Begriff Person resp. der
Mengenbeziehungen und v. v. in der einen der vier möglichen Standardformen
des kategorischen Urteils bzw. mittels Venn-Diagramme dargestellt werden
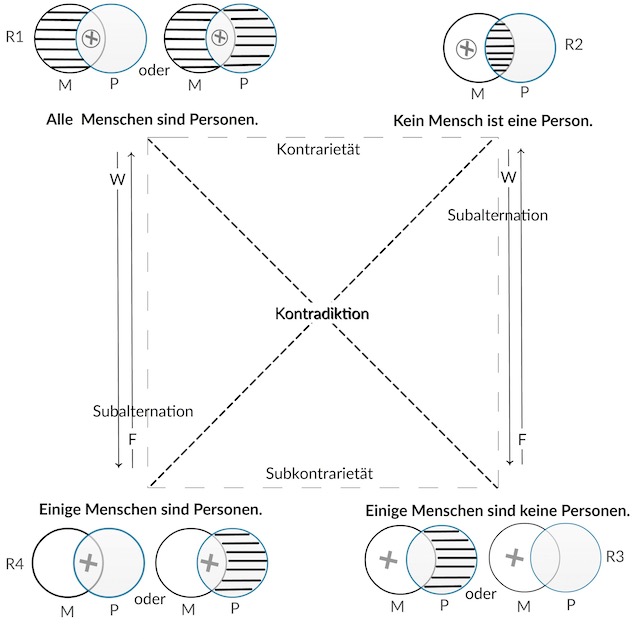
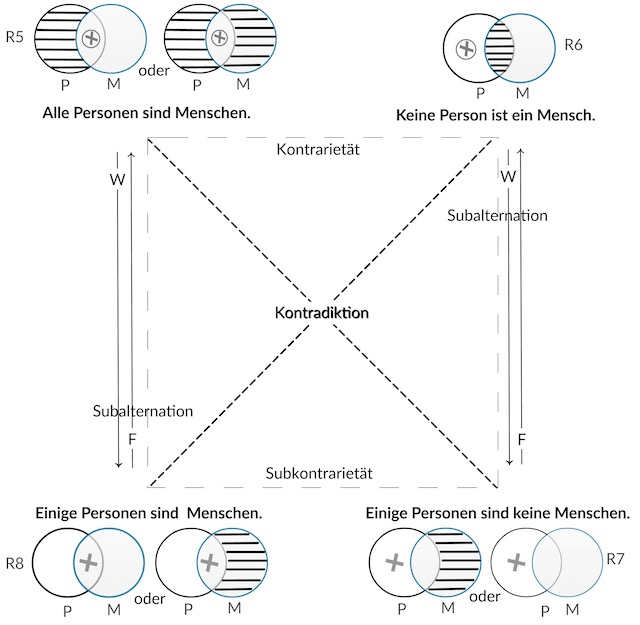
In den obigen Abb. werden mittels des traditionell interpretierten Logischen
Quadrates und in mengentheoretischer Hinsicht die spezifischen Beziehungen
zwischen dem Menschenbegriff und dem Personbegriff und v. v. dargestellt.
Die unterschiedlichen philosophischen Auffassungen zumVerhältnis zwischen
demMenschen- und Personbegriff sind insbesondere auf der Suche nach
bestimmten basalen Personbegriffen, die in sich durchaus unterschiedliche philosophische Ansichten vereinen können, wichtig.
Basale Relationen des Personbegriffs zum Menschenbegriff bzw. des Menschenbegriffs zum Personbegriff
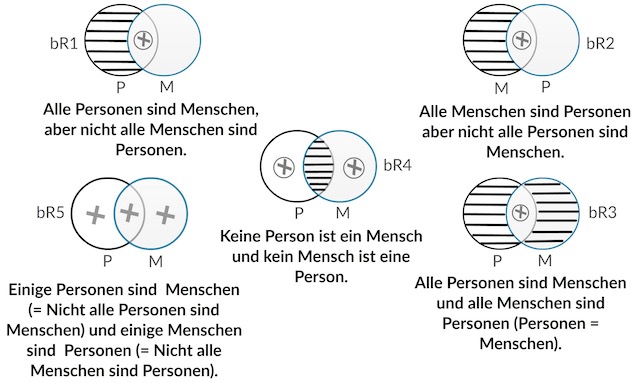
Im Rückgriff auf Erks Darlegungen sollen nun die durch die Venn-Diagramme (obige Abb.) visualisierten Mengenbeziehungen zwischen der Menge der Personen und derMenge derMenschen auf nichtweiter vereinfachbare Grundtypen resp. Grundmengen reduziert werden. Diese Aufgabe kann z. B. systematisch durchWahrheitstabellen und systematische Reduktion und dgl. gelöst werden oder auch durch die intuitiv-visuelleMethode. In den beiden obigen Abb. und gibt es zwischen den vier verschiedenen Urteilen bzw. Mengen bestimmte logische bzw. mengentheoretische Beziehungen, die in den beiden obigen Abb. verdeutlicht werden: Nämlich die kontradiktorische, die konträre, die subkonträre und die subalternative Beziehung. Innerhalb der konträren Beziehung muss mindestens ein Urteilssatz falsch sein: Wenn z. B. wahr ist, dass alleMenschen Personen sind (Wahrheitswert = 1), so muss logischnotwendig das Urteil, dass kein Mensch eine Person ist, falsch sein (Wahrheitswert = 0).Wenn aber innerhalb der konträren Beziehung schon ein Urteil falsch ist, so ist der Wahrheitswert des konträren Urteils unbestimmt. Innerhalb der subkonträren Beziehung muss mindestens ein Urteil wahr sein. Für die subkonträren Beziehung gelten somit m. m. die selben Gesetzmäßigkeiten wie für die konträre Beziehung.Werden für jedes einzelne der acht Urteile, die in den beiden obigen Abb. dargestellt sind, Wahrheitswert = 1 und Falschheitsswert = 0 eingesetzt und gefragt wird, wie sich die anderen Urteile bzw.Mengen hierzu verhalten, so könnte eine Wahrheitstabelle erstellt werden. Es soll hier nun die intuitiv-visuelleMethode in Angriff genommenwerden. Es gilt also, eine richtig Antwort auf die Frage zu finden, welche verschiedenen, möglichen Beziehungen kann es zwischen dem Person- und Menschenbegriff geben und v. v. bzw. welche verschiedenen möglichen Beziehungen kann es zwischen derMenge der Personen und der Menge der Menschen und v. v. geben. In den beiden obigen Abb. sind insgesamt 14 Venn-Diagramme abgebildet. Diese 14 Venn-Diagramme bilden alle möglichen mengentheoretischen Beziehungen zwischen derMenge der Personen und derMenge derMenschen und v. v. ab. Somit können anhand der in den beiden obigen Abb. dargestellten Venn-Diagramme alle möglichen Beziehungen zwischen demMenschen- und Personbegriff und v. v. bestimmtwerden. Gibt es also 14 verschiedene unterschiedliche Auffassungen bzgl. des Verhältnisses der beiden relevantenMengen?Werden die verschiedenenVenn-Diagramme miteinander verglichen, so fällt z. B. auf, dass eine logische resp. formale Äquivalenz zwischen R6 und R2 besteht (vgl. Abb. 3.6.). Überdies sind die Venn-Diagramme R4 (links) und R3 (rechts) und R8 (links) sowie R7 (rechts) in mengentheoretischer Hinsicht formal äquivalent, sodass sie auf einVenn-Diagramm reduziertwerden können. Die verbleibenden vier übrigenVenn-Diagramme der Subkontrarietät R4 (rechts) und R3 (links) und R8 (rechts) sowie R7 (links) sind mengentheoretisch mit anderenVenn-Diagramme äquivalent nämlich: R4 (rechts) und R3 (links) sind äquivalent zu R5 (links) und R8 (rechts). R7 (links) ist äquivalent zu R1 (links). Somit können diese vierVenn-Diagramme aufgrund ihrer Äquivalenz zu den beschriebenen Venn-Diagrammen gestrichen werden. Für die Subkontrarietät bleibt somit einVenn-Diagramm übrig. Ferner fällt auf, dass Venn-Diagramm R1 (rechts) zu R5 (rechts) äquivalent ist. So konnten die anfänglichen 14 Venn-Diagramme auf fünf basale Venn-Diagramme reduziert werden (vgl. obigen Abb). Wenn also die in den beiden obigen Abb. dargestellten Vendiagramme alle möglichen mengentheoretischen Beziehungen zwischen der Menge der Personen und der Menge derMenschen darstellten, so konnten nun die fünf grundlegenden d. h. nicht weiter reduzierbaren (basalen) Beziehungen zwischen dem Menschen- und dem Personbegriff und v. v. synoptisch bestimmt werden (vgl. obigie Abb.). Hiermit und insbesondere durch den Terminus basale Relationen ist auch mitausgesagt, das bR1-bR5 sich gegenseitig einsichtigerWeise ausschließen d. h. entweder ist bR1 wahr (ausschließendes Oder) bR2 bR3 bR4 bR5. Welche basale Relation aber wahr und welche falsch ist, lässt sich nicht rein formell, sondern nur materialiter feststellen.